The craft of a conlanger
Having been developed over two centuries, the language of continuum mechanics is still not perfect and contains (knowledge) gaps in its grammar. Such grammatical gaps result in theories that are empirically applicable to only a subset of materials and fail in other scenarios. Thus, I enrich the field of continuum mechanics by grounding its theories in the first principles of physics. To this end, I lead a research group at the Department of Continuum Mechanics, RWTH Aachen University, Germany, focused on establishing (1) original continuum-mechanics domain-knowledge to enable the creation of interpretable machine-learning models, and (2) statistical-learning framework of large mechanical datasets. My key contributions to the domain knowledge include: Analytical homogenization (Ah), Analytical Inelasticity (AI), and Thermodynamic Regularization (THERE).
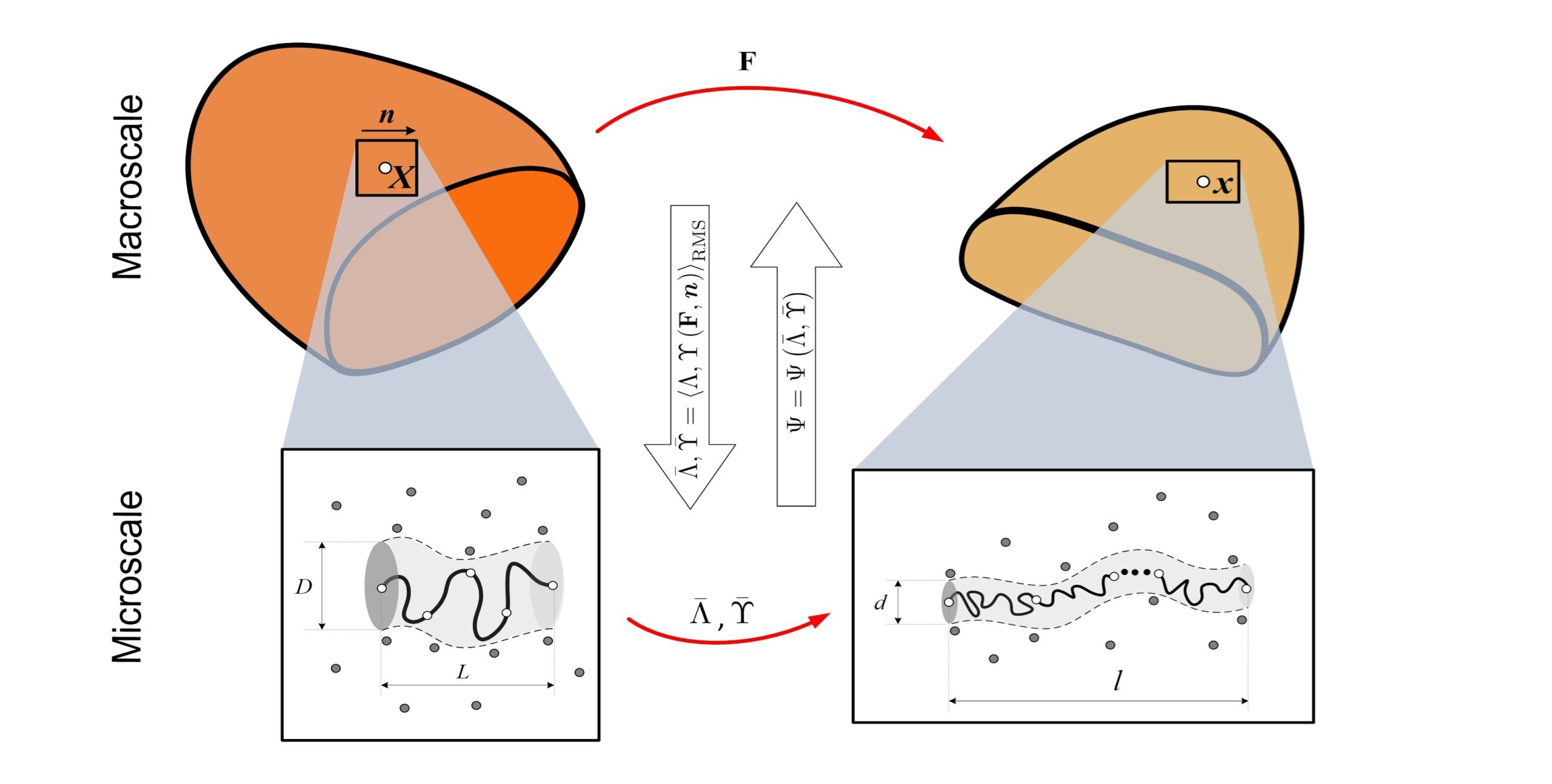
“Ah” (analytical homogenization) is a statistical homogenization scheme, so-called mean field theory, that yields analytical microscopic strain measures for solving multiscale boundary value problems in diverse soft materials characterized by both solid-like and shell-like behavior and a wide range of mechanical phenomena (nonlinear elasticity, anisotropic damage, phase transition and fiber sliding). Such homogenization scheme offers physically based strain invariants that automatically guarantee interpretable and realistic behavior (such as non-affine deformation, material objectivity and material symmetry) in material models. The Ah method is particularly powerful in the age of data science, as it allows for the selection of material models without artificial restrictions, while maintaining the physical interpretability of results.
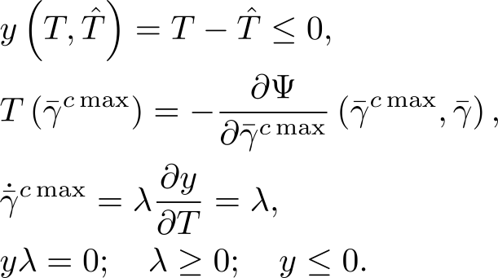
“AI” (analytical inelasticity) is a nonlinear inelasticity theory describing the evolution of internal variables for any irreversible process in continuum mechanics. “AI” relies on a single thermodynamic potential, specifically the Helmholtz free energy, and achieves accuracy and performance efficiency in computing internal variables through analytical methods. This theory is applicable to a wide range of soft materials, including elastomers, hydrogels, and textile reinforcements. Notably, AI is effective for modeling natural rubbers and any strain-induced crystallizing polymers, materials for which the traditional double potential theory is inadequate.
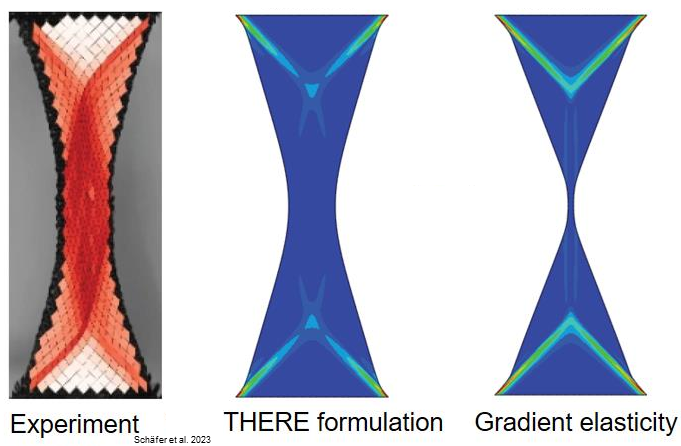
“THERE” is a thermodynamically based regularization technique that addresses ill-posed problems in solid mechanics across a wide range of materials, while ensuring the interpretability and measurability of the regularization parameters. Its name reflects the adherence to the laws of thermodynamics and a single thermodynamic potential (i.e., the Helmholtz free energy). Notably, THERE is effective for deformation-induced phase transition in natural rubbers and crystallizing polymers, a phenomenon for which the traditional gradient damage and phase field methods are inadequate.
